這是我為密碼學期中報告整理的筆記,記錄一下我對公鑰加密的理解。還有很多地方需要再修改,先記下來慢慢完善~
今天的學習心得
今天花了一整天研究公鑰密碼系統,說真的這些數學概念真的很燒腦!但漸漸開始理解為什麼這些系統如此重要了。想想看,我們每天在網路上的安全通訊,從網購、銀行交易到私人訊息,全都仰賴這些看似抽象的數學原理。
四種主要的公鑰系統各有特色,也各有適用場景。這篇筆記主要記錄RSA、Diffie-Hellman、ElGamal和橢圓曲線密碼學這四種系統的基本原理和比較。不是嚴謹的學術論文,只是我自己學習過程的整理~
RSA:最廣為人知的公鑰系統
RSA是我最早接觸的公鑰系統,由Rivest、Shamir和Adleman三位學者在1970年代後期發明。它的安全性基於一個簡單但強大的數學難題:大整數分解。
簡單來說,RSA的運作原理是:
- 選兩個超大質數p和q,相乘得到n
- 計算(p-1)(q-1)的值,稱為φ(n)
- 選一個與φ(n)互質的數e作為公鑰的一部分
- 計算d使得e*d除以φ(n)餘1
- 公鑰是(n,e),私鑰是(n,d)
加密時,假設明文是M,就計算M的e次方除以n的餘數,得到密文C。
解密時,計算C的d次方除以n的餘數,就能還原成M。
今天的電腦要分解一個2048位元的大整數仍然需要千萬年計算時間,這就是RSA安全性的來源。不過,RSA運算較慢,特別是解密過程,所以通常用於數位簽章或加密對稱金鑰,而不是直接加密大量資料。
Diffie-Hellman:安全的密鑰交換
研究了一下Diffie-Hellman協議,發現它其實不是用來加密訊息的,而是讓兩個人在不安全的通道上協商出一個共同的密鑰。這個協議在1976年提出時真的是革命性的突破!
Diffie-Hellman的巧妙之處在於,即使有人監聽了全部的通訊內容,也無法算出最終的共享密鑰。它的安全性基於離散對數問題的困難度。
運作方式像是:
- Alice和Bob先約定兩個公開數字:一個質數p和一個生成元g
- Alice私下選一個數字a,計算A = g的a次方除以p的餘數,然後把A發給Bob
- Bob私下選一個數字b,計算B = g的b次方除以p的餘數,然後把B發給Alice
- Alice收到B後,計算B的a次方除以p的餘數
- Bob收到A後,計算A的b次方除以p的餘數
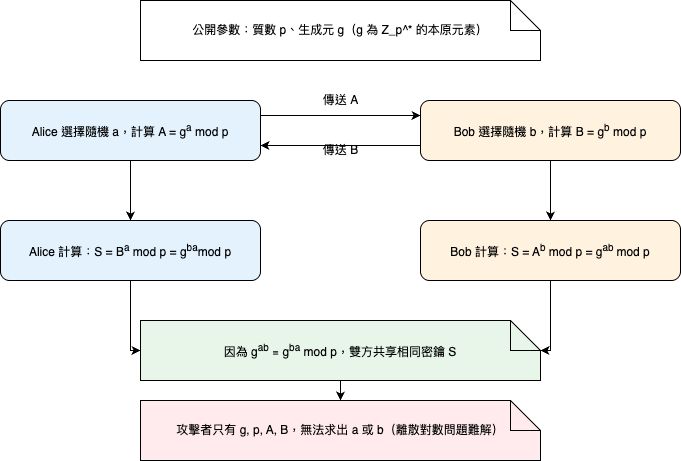
神奇的是,雙方計算出的結果是相同的!這就成為他們的共享密鑰。
但是Diffie-Hellman有個缺點,它不能驗證通訊對象的身份,所以容易受到中間人攻擊。在實際應用中,通常需要結合其他機制來解決這個問題。
ElGamal:具有特殊性質的加密系統
ElGamal系統是1985年由Taher ElGamal提出的,它基本上是Diffie-Hellman的擴展版,形成了一個完整的加密系統。
ElGamal系統的特別之處在於它具有「同態性」—這是一個超酷的特性!它允許對密文進行特定運算,從而實現對相應明文的運算,而無需先解密。比如,兩個密文相乘後解密,等同於兩個明文相乘。這在某些應用場景非常有用,如電子投票和隱私保護計算。
不過ElGamal的缺點是密文長度會變為明文的兩倍,而且計算開銷比RSA大。
橢圓曲線密碼學:未來之星
最近幾年,橢圓曲線密碼學(ECC)越來越受歡迎,原因很簡單:它效率高!
ECC基於橢圓曲線上的點運算,相比RSA和傳統Diffie-Hellman,在相同安全性下需要的密鑰長度小很多。例如,256位元的ECC密鑰安全性相當於3072位元的RSA密鑰。這在資源有限的設備上特別有價值。
比特幣和其他加密貨幣就使用了基於ECC的數位簽章算法。想想看,每次比特幣交易都依賴於橢圓曲線數學,這真的很神奇!
四種系統的比較
整理了一下這四種系統的優缺點:
RSA
- 優點:廣泛部署,加密操作快
- 缺點:密鑰較長,解密操作慢
Diffie-Hellman
- 優點:提供完美前向保密性
- 缺點:僅用於密鑰交換,需額外認證機制
ElGamal
- 優點:具有同態特性
- 缺點:密文膨脹,計算較慢
ECC
- 優點:高效率,小密鑰
- 缺點:實現較複雜,專利問題(某些曲線)
量子計算的威脅
最近很擔心的一個問題是量子計算機的發展。Shor演算法理論上可以在多項式時間內解決整數分解和離散對數問題,這意味著它能破解所有這四種加密系統!
幸好密碼學家們已經在研發「後量子密碼學」,設計能抵抗量子計算攻擊的新密碼系統。美國NIST已經在進行標準化過程,選定了幾個候選算法。
在這段過渡期,業界正採用混合方案:同時使用傳統公鑰算法和後量子算法,以確保安全性。
學習心得
研究這些密碼系統真的讓我對數學有了新的敬意。這些看似抽象的數學問題,竟然能夠保護我們的數位世界安全!
下周打算深入研究一下實際應用案例,特別是TLS協議如何使用這些密碼系統。還要試著自己實現一個簡單的RSA加密程序,實踐出真知嘛!
希望期中報告能順利完成,下次再來更新進度~